引言
为什么选择分享编译原理
- 第一,以前我看过编译原理书籍,太难了,学不动,但这次选为分享主题,准备分享是一个深度学习的过程,对我来说不光是分享知识,同时也是克服困难的过程
正则表达式也是,分享完之后好像看我挺懂,其实我就是因为不懂我就要去学习然后分享
- 第二,实用性,如果对我们没有实用价值(用来理解我们的技术、直接运用在项目中的技术),那在当前就没有太大的学习必要
学习编译原理可以理解我们的编程语言,可以了解到一些底层库的实现原理,在下面应用场景中会有举例
这篇分享的整个流程,我会从概念切入,原理实现,再到实战应用上来使用编译原理解决应用问题
知识点
通过本文你将会收获如下内容:
编译原理应用场景 编译原理的整个过程概览 词法分析器、语法分析器的原理实现 实战:使用 开源词法分析器 flex、语法分析器 bison 解析表达式跟 SQL 语法
应用场景
编译原理研究的是如何将源代码转换为目标代码(机器语言或中间代码)的过程
编程语言
C++, Java, Javascript
对于机器而言,代码就是一串字符,如何将这串字符想要表达的含义告诉机器
这就是编译原理要做的事情

运行

要开发一门编程语言就需要学习编译原理
抽象语法树(AST)
AST 在编译原理中是属于词语法分析后的产物,也就是说实现一个 AST 解析库需要学习词法分析和语法分析,所以我这次分享深入的点就是词法、语法分析
一些 Javascript AST 解析库
基于这些库的使用我们又能做的事情
- 应用开发中,语言降级处理
- 代码检查工具:eslint
- 其他用途,例如 typescript-json-schema,将 typescript 类型 转换为 json-schema,可以在服务端实现 API 文档自动生成能力
DSL 领域特定语言
针对特定领域开发的专用语言,通常专注于解决特定领域的问题,因此可以提供更简洁、易于理解和易于使用的语法和工具
- SQL 结构化查询语言:Mysql,ES...
- HTML/CSS
- 正则表达式: 字符串匹配 DSL
- YAML/JSON:数据序列化和配置文件的DSL
- Excel:公式表达式
- JSX 语法
甚至我们可能在自己的领域下,也会有 DSL 语言的开发需求
编译的整个阶段
在现代编译原理-虎书中,编译原理实际是在讲述现代编译器的整个构成
它包含词法分析、语法分析、抽象语法、语义分析、中间代码表示、指令选择、数据流分析、寄存器分配以及运行时系统等等
但我们平常比较关注的是 词法分析、语法分析、语义分析、中间代码表示、优化、目标代码生成这些过程

词法分析
简短的说:词法分析是将输入分解成一个个独立的词法符号: 单词符号(token)
你可以理解为原本这串代码里的原子化是每个字符,词法分析后原子化最小粒度为我们定义的每个 Token
下面这段 Js Token 化:
let a = 10
b + 20Token:
VariableDeclaration(let)
Identifier(a)
Assignment
Literal(10)
Identifier(b)
BinaryExpression(+)
Literal(10)图解:
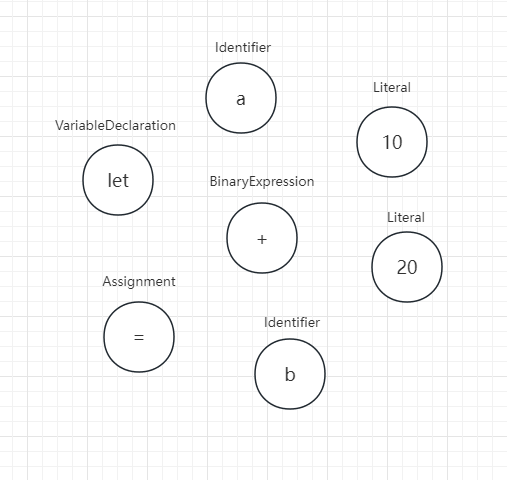
语法分析
语法分析是将单词符号连接成语句,并生成抽象语法树
在词法分析过后,再经历语法分析将 原子化 Token 连接起来构造成 AST 抽象语法树
构造成AST 抽象语法树之后,我们就可以在程序上做处理,比如直接解释执行
例如:
let b = a + 10变量声明语句,声明类型 let,变量标识符 b,初始化表达式 a + 10
有 AST 之后,也可以选择解释运行
对应的 AST 树

通过 astexplorer 可以在线将代码解析为抽象语法树
生成抽象语法树是将我们代码用一种清晰、易于处理的方式表示
AST 对于我们前端的重要性,例如 babel,将 es6 转 es5,他里面的 babel-parser 即是一个语法分析器
eslint 在 AST 基础上做静态检查
一些跨端框架,Taro、MorJS、React-Native,将 Jsx 转换为 AST 语法树,在转换为 React.createElement() 方法调用

语义分析
语义分析阶段是对源代码进行深层次的上下文分析,以确定代码的语法结构和语义含义是否正确
这中间涉及到:
类型检查:对标识符类型进行检查,像强类型语言,会检查标识符在使用前是否声明,操作符和操作数之间类型是否兼容,Typescript 的出现就 为 Javascript 增强了这一能力,完备的类型系统
例如:这段代码,在语法分析中并无异常,描述变量 str 赋值给 num,但在语义上来说,str 类型与 num 不兼容,可能会产生错误
Javascriptlet str: string = 1; let num: number = str;作用域检查:验证标识符的作用域和可见性,检查变量、函数在哪个作用域下可以访问,像外层无法访问里层作用域中的变量
例如函数中引用的变量应该指向到哪里,在语义分析中需要确定每个变量的可见范围,以及在哪里可以访问与修改
Javascriptlet person1 = 'xjq' function play() { let person1 = 'xjq2' let person2 = 'xjq3' console.log(person1) } console.log(person2)错误检查和报告:检查源代码中的语义错误,并生成相应的错误信息,在我们开发中是最熟悉的,类型不匹配、变量函数未声明、作用域访问问题等,错误信息可以帮我们调试和修复代码问题

语义分析是接着语法分析阶段,对抽象语法树进行进一步的处理
他的输出通常是一个经过验证和转换的 AST 抽象语法树
为后续优化与代码生成阶段做准备
中间代码生成
抽象层
经过前面的分析之后,编译器可以直接去解释执行 抽象语法树,或者直接生成目标代码,但我们需要跑在不同的系统上面,各个系统 CPU 架构又不相同,我们还需要对应生成不同的汇编代码
所以在这中间我们新增了一层抽象:中间代码 IR,统一优化后生成中间代码,再由中间代码生成目标代码
中间代码的两个用途:
解释执行
解释型语言,像 JavaScript、Python,生成中间代码后,可以直接解释和执行,但是运行效率比较低,因为在运行时需要逐行解释和执行
代码优化
生成代码之后的优化工作,不同 CPU 体系的汇编语言不同,没必要在汇编代码上去做这些优化,可以基于 IR 使用统一的算法来完成,来降低编译器适配不同 CPU 的复杂性
优化
优化阶段是对中间代码进行各种优化操作,来提高程序的执行效率和性能
优化器可能包含常量传播、复制传播、删除无用代码、循环优化等技术,来生成更高效的代码
这里来稍微解释下这些技术
常量传播
它是通过识别代码中的常量表达式,将其替换为计算结果的常量值,来减少运行时的计算量
cppint x = 5; int y = x + 3; int z = y * 2;经过优化之后
cppint z = 16;复制传播
复制传播技术是识别变量复制操作,将变量的值复制到使用该变量的地方,来减少变量访问次数,可以减少内存读取操作,提高执行效率
在底层寻址也是耗时操作,我们要使用变量 y,先找到 y 的地址,再去找 x 的地址,可以将中间过程优化掉
cppint x = 5; int y = x; int z = y * 2;优化后
cppint z = x * 2;删除无用代码
懂的都懂,一些对输出结果没有什么影响的代码,可以直接删除
循环优化
比如循环展开与合并,将多个循环迭代合并
cppint sum = 0; for (int i = 0; i < 100; i++) { sum += i; }优化为
sum = 0 + 1 + 2 + 3 + ... + 99来减少循环开销和分支开销
目标代码生成
将优化后的中间代码转换为特定目标平台的机器码或汇编代码
扩展:LLVM,LLVM(Low-Level Virtual Machine)是一个开源的编译器基础设施项目,提供了一组用于编译、优化和执行程序的工具和库
LLVM提供了一套灵活的编译器基础设施,可以用于构建各种编译器
- 传统的静态编译器:在代码编写完成后编译成机器码,像 C、C++、Java(部分静态编译)
- 即时编译器(JIT):在运行时将中间代码编译成机器码,并缓存以供重复使用,Java 使用 JIT 编译器将字节码编译成机器码,一些 JS引擎也会采用即时编译器提升性能
- 解释器:解释器在运行时逐行解释和执行源代码,没有预先编译过程,所以执行速度通常比较慢,但是它更加灵活,因为不需要生成特定平台的机器码
JIT:
运行过程中,JIT 编译器会将 add 转换成机器码,并缓存起来,下次程序调用时,可以直接使用缓存的机器码,无需重新编译
JIT编译器可以根据程序运行时的上下文信息来优化,例如在循环中,某个变量值始终不变,那么编译器可以将它缓存起来,避免重复计算
function add(a, b) {
return a + b
}
let x = 1
let y = 2
let z = add(x, y)
console.log(z)词法分析器
先看看这段 js 代码经过词法分析器分析后的结果图解
let a = 10
let b = a + 20转换
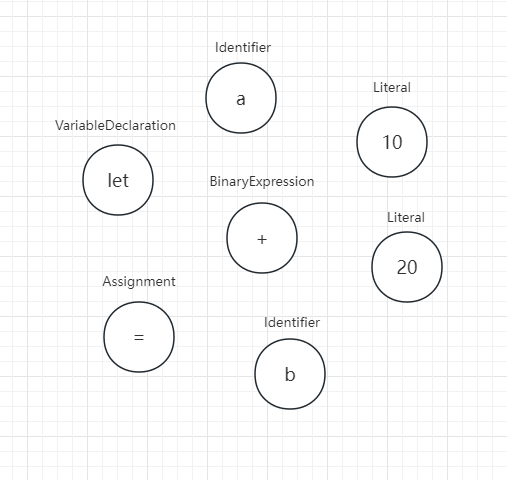
实现一个词法分析器需要先了解下什么是有限状态自动机
有限状态自动机
有限状态自动机是一种计算模型,用于描述由有限个状态和转移函数组成的计算机系统
有限状态自动机可以分为两种类型:确定性有限状态机(DFA)和非确定性有限状态机(NFA)。
DFA 中,从一个状态出发,对于每个输入符号,只有一条转移路径可以被执行。而在 NFA 中,从一个状态出发,对于每个输入符号,可能有多条转移路径可以被执行
有限状态自动机的核心思想是状态转换,即在给定输入的情况下,系统从一个状态转移到另一个状态。
通俗的说:状态机里面包含 N 多个状态,每次喂给它一个字符,就会有一些状态扭转,在词法分享中,状态就是 每个 Token 以及一些 Token 的过渡状态
我们把 Token,以及 Token 的每一部分都看做是一个状态
比如 let 是终结状态, le 是 let 的一个过渡状态,当前为 le 状态,下一个字符为 t 时才会扭转到终结态 let,否则可能就是一个变量,lee、lel 等等
在下面案例有一些图解来看看状态机怎么协助我们提取 Token 的
案例分析一
这里使用 C++、Java 的一个 int 类型变量声明与赋值,以及相加与相乘操作符 作为例子
int a = 2;
int b = 3;
int ia = 4;上述代码的有限状态机:
蓝色底色为 终结态,无法继续扭转状态,带有自循环箭头代表可以继续接收字符,但是状态始终为 Id
状态 1 为初始态
输入 字符 i 进入状态 2:Int1
再次扭转输入 n 进入 Int2,非 n 字符 进入 状态 5:Id
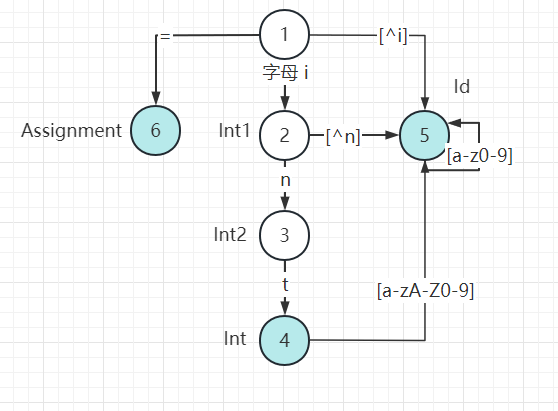
代码在 token1 目录
使用 TS 代码实现上述状态机:
状态定义:
包含过渡状态与终结状态
// 状态机状态定义, 过度状态不是最终状态,自动生成数字
enum DfaState {
Initial,
Int1,
Int2,
Assignment = 'Assignment',
SemiColon = 'SemiColon',
IntLiteral = 'IntLiteral',
Id = 'Id',
Int = 'Int',
}定义 Token 对象:
每个 Token 包含 类型, 对应上面的枚举状态,text 是 附加属性,例如 变量 的 text 值就是变量名
class Token {
// token 附加字段,比如 IntLiteral 需要额外存储数据
text?: string
// 状态类别,对应状态机中的终结状态
type: DfaState
constructor(type: DfaState, text?: string) {
if (text) this.text = text
this.type = type
}
}词法分析器:
function isAlpha(ch: string) {
return /[a-z]/i.test(ch)
}
function isNumber(ch: string) {
return /\d/.test(ch)
}
function isBlank(ch: string) {
return /\s|\n/.test(ch)
}
export function tokenize(str: string) {
let state: DfaState = DfaState.Initial
const tokens: Token[] = []
// 临时变量, 用于存储一些字面量字符
let text = ''
// 每次解析完一个 token 后需要重置 状态 跟临时变量
const push = function (...items: Token[]) {
text = ''
state = DfaState.Initial
return tokens.push(...items)
}
for (let i = 0; i < str.length; i++) {
const ch = str[i]
switch (state) {
// 初始状态
case DfaState.Initial:
if (isAlpha(ch)) {
if (ch === 'i') {
state = DfaState.Int1
} else {
state = DfaState.Id
}
text += ch
} else if (isNumber(ch)) {
text += ch
state = DfaState.IntLiteral
} else if (ch === '=') {
push(new Token(DfaState.Assignment))
}
break
case DfaState.Int1:
if (ch === 'n') {
state = DfaState.Int2
} else {
state = DfaState.Id
}
text += ch
break
case DfaState.Int2:
if (ch === 't') {
push(new Token(DfaState.Int))
} else {
state = DfaState.Id
text += ch
}
case DfaState.Id:
if (ch === ';') {
push(new Token(DfaState.Id, text))
push(new Token(DfaState.SemiColon))
} else if (isBlank(ch)) {
push(new Token(DfaState.Id, text))
}
break
case DfaState.IntLiteral:
if (isBlank(ch) || ch === ';') {
push(new Token(DfaState.IntLiteral, text))
} else {
text += ch
}
break
default:
}
}
return tokens
}测试验证:
import { tokenize } from './index'
const str = ` int a = 20;
int b = 3;`
console.log(tokenize(str))不出意外的话,输出该代码的 token 序列如下:
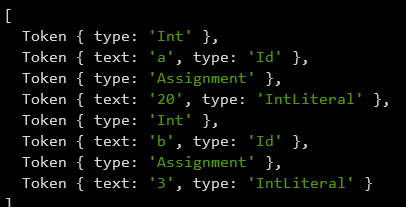
案例分析二
词法分析器能力增强
- 比较、算数(+、*)操作符解析
- 布尔、字符串变量
待解析 code:
int c = a + 10;
int d = a * 2;
bool bool1 = a > b;
bool bool2 = c >= d;状态图分析:
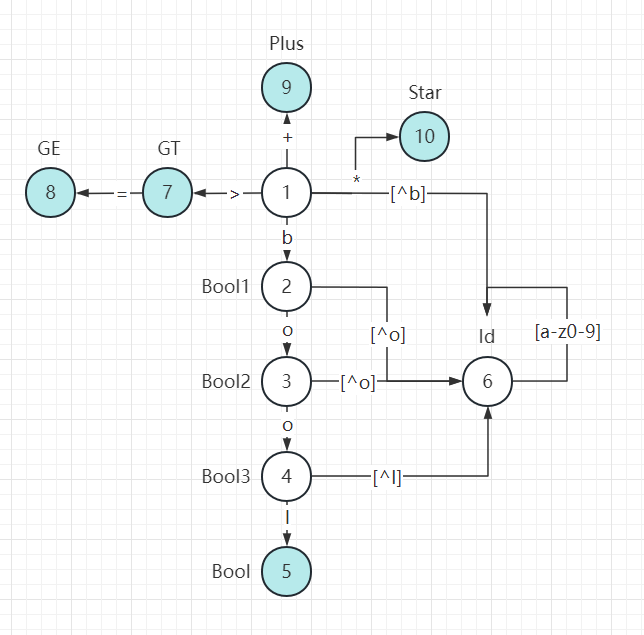
代码在 token2 目录
使用 TS 代码实现上述状态机:
enum DfaState {
Initial,
Int1,
Int2,
Bool1,
Bool2,
Bool3,
IntLiteral1,
Assignment = 'Assignment',
Plus = 'Plus',
Star = 'Star',
GT = 'GT',
GE = 'GE',
SemiColon = 'SemiColon',
IntLiteral = 'IntLiteral',
Id = 'Id',
Int = 'Int',
Bool = 'Bool',
}
class Token {
text?: string
type: DfaState
constructor(type: DfaState, text?: string) {
if (text) this.text = text
this.type = type
}
}
function isAlpha(ch: string) {
return /[a-z]/i.test(ch)
}
function isNumber(ch: string) {
return /\d/.test(ch)
}
function isShutDown(ch: string) {
return /\s|\n|[;]/.test(ch)
}
function isIdentifier(ch: string) {
return isAlpha(ch) || isNumber(ch)
}
export function tokenize(str: string) {
let state: DfaState = DfaState.Initial
const tokens: Token[] = []
let text = ''
const push = function (...items: Token[]) {
text = ''
state = DfaState.Initial
return tokens.push(...items)
}
for (let i = 0; i < str.length; i++) {
const ch = str[i]
switch (state) {
case DfaState.Initial:
if (isAlpha(ch)) {
if (ch === 'i') {
state = DfaState.Int1
} else if (ch === 'b') {
state = DfaState.Bool1
} else {
state = DfaState.Id
}
text += ch
} else if (isNumber(ch)) {
text += ch
state = DfaState.IntLiteral1
} else if (ch === '=') {
push(new Token(DfaState.Assignment))
} else if (ch === '+') {
push(new Token(DfaState.Plus))
} else if (ch === '*') {
push(new Token(DfaState.Star))
}
break
case DfaState.IntLiteral1:
if (isShutDown(ch)) {
push(new Token(DfaState.IntLiteral, text))
}
text += ch
break
case DfaState.Int1:
if (ch === 'n') {
state = DfaState.Int2
} else {
state = DfaState.Id
}
text += ch
break
case DfaState.Int2:
if (ch === 't') {
push(new Token(DfaState.Int))
} else {
state = DfaState.Id
text += ch
}
break
case DfaState.Id:
if (isShutDown(ch)) {
push(new Token(DfaState.Id, text))
if (ch === ';') {
push(new Token(DfaState.SemiColon))
}
} else if (isIdentifier(ch)) {
text += ch
}
break
case DfaState.Bool1:
if (ch === 'o') {
state = DfaState.Bool2
text += ch
} else if (isShutDown(ch)) {
push(new Token(DfaState.Id, text))
if (ch === ';') {
push(new Token(DfaState.SemiColon))
}
} else if (isIdentifier(ch)) {
state = DfaState.Id
}
break
case DfaState.Bool2:
text += ch
if (ch === 'o') {
state = DfaState.Bool3
} else if (isShutDown(ch)) {
push(new Token(DfaState.Id, text))
if (ch === ';') {
push(new Token(DfaState.SemiColon))
}
} else if (isIdentifier(ch)) {
state = DfaState.Id
}
break
case DfaState.Bool3:
text += ch
if (ch === 'l') {
state = DfaState.Bool
} else if (isShutDown(ch)) {
push(new Token(DfaState.Id, text))
if (ch === ';') {
push(new Token(DfaState.SemiColon))
}
} else if (isIdentifier(ch)) {
state = DfaState.Id
}
break
case DfaState.Bool:
if (isShutDown(ch)) {
push(new Token(DfaState.Bool))
if (ch === ';') {
push(new Token(DfaState.SemiColon))
}
} else if (isIdentifier(ch)) {
text += ch
state = DfaState.Id
}
break
default:
}
}
return tokens
}测试验证代码:
import { tokenize } from '.'
const str = ` int c = a + 10;
int d = a * 2;
bool bool1 = a > b;
bool bool2 = c >= d;`
console.log(tokenize(str))输出 Token 结果
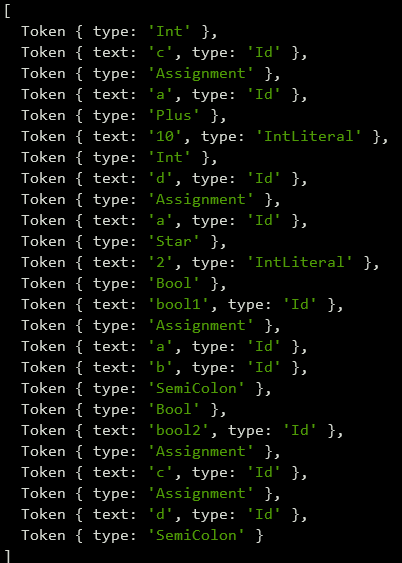
完备的词法分析器的使用
实际应用中想要实现一个完备的词法分析器还是很复杂的,有限状态自动机将变的很复杂
还好开源社区有一些比较完备的库,我们可以通过它来实现一个脚本语言的 Token 解析
词法分析器 flex
我这里将跑几个例子看看效果
flex 词法分析器的使用
环境: Mac
安装:
brew install flexflex 文件分成三个主要部分
- 定义部分:包含一些全局设置和声明
- 规则部分:词法分析规则
- 用户代码:自定义处理逻辑
自定义处理逻辑部分会有少量 C++ 代码,但是大都是各语言通用的基础语法
主要还是规则部分,需要为想要提取的 Token 编写正则表达式
代码在 flex1 目录
新建 lexer.l 文件
%{
#include <iostream>
using namespace std;
%}
%option noyywrap
%{
int yylval;
%}
%{
#define INTEGER 257
%}
%%
[0-9]+ { yylval = atoi(yytext); return INTEGER; }
[\+\-\*/\(\)] { return yytext[0]; }
[ \t\n] { /* ignore whitespace */ }
. { cerr << "Invalid token: " << yytext << endl; }
%%
int main(int argc, char** argv) {
int token;
while ((token = yylex())) {
cout << "Token: " << token;
if (token == INTEGER) {
cout << ", Value: " << yylval;
}
cout << endl;
}
return 0;
}编译:
flex lexer.l
# 编译成可执行文件
g++ -o lexer lexer.l运行:
./lexer这些规则可以处理一些操作符以及数字字面量的 Token
10 + 20
20 / 2
1234我们加强一下
就拿 Excel 一些函数来当例子
=SUM(A1:A10)
=AVERAGE(A1:A10)
=IF(A1>10, "大于10", "小于等于10")
=LEFT(A1, 3)预先分析一波:
- 关键词 提取 =、SUM、AVERAGE、IF、LEFT
- A1、A10定义为 ID
- 双引号中的定义为 STRING 字面量
- 3、10 定义为 INTEGER 字面量
代码在 flex2 目录
修改 lexer.l 文件,加入对应 Token 解析规则
%{
#include <iostream>
#include <string>
using namespace std;
%}
%option noyywrap
%{
int yylval;
string yylstr;
%}
%{
#define INTEGER 257
#define STRING 258
#define SUM 260
#define AVERAGE 261
#define IF 262
#define LEFT 263
#define COMMA 264
#define ID 265
%}
%%
SUM { return SUM; }
AVERAGE { return AVERAGE; }
IF { return IF; }
LEFT { return LEFT; }
, { return COMMA; }
[a-zA-Z_][a-zA-Z0-9_]* { yylstr = yytext; return ID; }
\"[^\"\n]+\" { yylstr = yytext; return STRING; }
[0-9]+ { yylval = atoi(yytext); return INTEGER; }
[\+\-\*/\(\)] { return yytext[0]; }
[ \t\n] { /* ignore whitespace */ }
. { cerr << "Invalid token: " << yytext << endl; }
%%
int main(int argc, char** argv) {
int token;
while ((token = yylex())) {
switch(token){
case IF:
case LEFT:
case SUM:
case AVERAGE:
case COMMA:
cout << "Token: " << token;
break;
case INTEGER:
cout << "Token: " << token;
cout << ", Value: " << yylval;
break;
case STRING:
case ID:
cout << "Token: " << token;
cout << ", Value: " << yylstr;
break;
}
cout << endl;
}
return 0;
}tokenizr 词法分析器的使用
tokenizr 是 Js 驱动的词法分析器,使用简单方便
语法分析器
语法分析难度提升一个量级
案例分析:加法表达式
代码在 ast1 目录中
示例:
1 + 2AST 图:
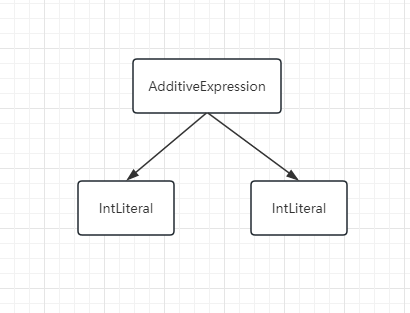
它的抽象语法树是由 表达式节点+两个字面量子节点组成
预测分析
通过预读一个 Token 识别当前语句
代码实现:
import { DfaState, Token } from '../token2'
// 节点类型
enum ASTNodeType {
Program = 'Program',
IntLiteral = 'IntLiteral',
Variable = 'Variable',
AdditiveExpression = 'AdditiveExpression',
}
/**
* 读取 Token 的 Reader 类
*
* @class TokenReader
*/
class TokenReader {
tokens: Token[]
pos = 0
constructor(tokens: Token[]) {
this.tokens = tokens
}
/**
* 向前预读一个 Token
*
* @return {*}
* @memberof TokenReader
*/
peek() {
return this.tokens[this.pos]
}
/**
* 消耗一个 Token
*
* @return {*}
* @memberof TokenReader
*/
read() {
return this.tokens[this.pos++]
}
}
/**
* 节点类, 每个节点拥有类型,跟子节点,子节点暂且为数组
* text 为节点值的存放
*
* @class ASTNode
*/
class ASTNode {
type: ASTNodeType
text?: string
children?: (ASTNode | null | undefined)[]
constructor(type: ASTNodeType, text?: string) {
this.type = type
this.text = text
}
addChild(child?: ASTNode | null) {
if (!this.children) this.children = []
this.children.push(child)
}
}
export class AST {
tokenReader: TokenReader
error: string[] = []
warn: string[] = []
constructor(tokens: Token[]) {
this.tokenReader = new TokenReader(tokens)
}
build() {
const root = new ASTNode(ASTNodeType.Program)
root.addChild(this.additive(this.tokenReader))
return root
}
/**
* 加法表达式处理
*
* @param {TokenReader} tokenReader
* @return {*}
* @memberof AST
*/
additive(tokenReader: TokenReader) {
let child1
const peekToken = tokenReader.peek()
if (peekToken && peekToken.type === DfaState.IntLiteral) {
const token = tokenReader.read()
child1 = new ASTNode(ASTNodeType.IntLiteral, token.text)
}
if (child1) {
const peekToken = tokenReader.peek()
if (peekToken && peekToken.type === DfaState.Plus) {
tokenReader.read()
let child2
const peekToken = tokenReader.peek()
if (peekToken && peekToken.type === DfaState.IntLiteral) {
const token = tokenReader.read()
child2 = new ASTNode(ASTNodeType.IntLiteral, token.text)
}
if (child2) {
const node = new ASTNode(ASTNodeType.AdditiveExpression)
node.addChild(child1)
node.addChild(child2)
child1 = node
} else {
throw new Error('无法解析加法表达式!')
}
}
return child1
}
return null
}
}测试验证:
import { tokenize } from '../token2'
import { AST } from './index'
let str = '1 + 1;'
const tokens = tokenize(str)
console.log(tokens)
const ast = new AST(tokens)
console.log(JSON.stringify(ast.build(), null, 4))输出:

递归下降分析
递归下降算法是一种自顶向下的语法分析方法,它的基本思想是将语法规则转化为一组递归函数,每个函数对应一个非终结符号,并依次处理输入的符号流
比如说加法表达式形式 如: exp + exp 这里 exp 如果是 number 那么就是 1 + 1 这种
1 + 1 + 2 这种属于 exp + number,我们需要递归对 exp 进行处理
递归分析加法表达式
代码在 ast2 目录中
多个值的加法表达式
1 + 2 + 3;AST 树:确定结合性,加法是左结合的,所以从左向右,前两个字面量先结合
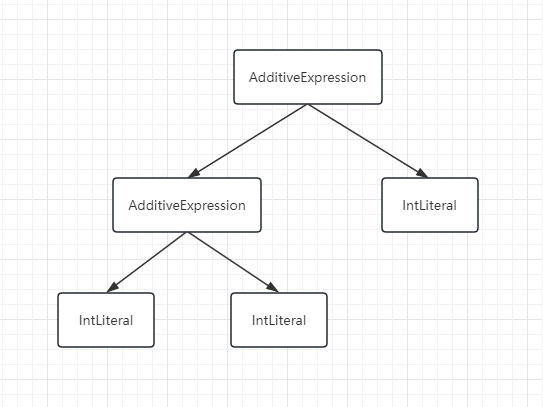
将 ast1 改为 递归处理
/**
* 加法表达式处理
*
* @param {TokenReader} tokenReader
* @return {*}
* @memberof AST
*/
additive(tokenReader: TokenReader): any {
let left = this.primary(tokenReader);
let rootNode: ASTNode | null = left;
if (left) {
const peekToken = tokenReader.peek();
if (peekToken && peekToken.type === DfaState.Plus) {
const node = new ASTNode(ASTNodeType.AdditiveExpression);
tokenReader.read();
const right = this.additive(tokenReader);
if (right) {
node.addChild(left);
node.addChild(right);
rootNode = node;
} else {
throw new Error('无法解析加法表达式!');
}
}
}
return rootNode;
}测试验证:
import { tokenize } from '../token2'
import { AST } from './index'
let str = '1 + 1 + 3;'
const tokens = tokenize(str)
console.log(tokens)
const ast = new AST(tokens)
console.log(JSON.stringify(ast.build(), null, 4))输出:
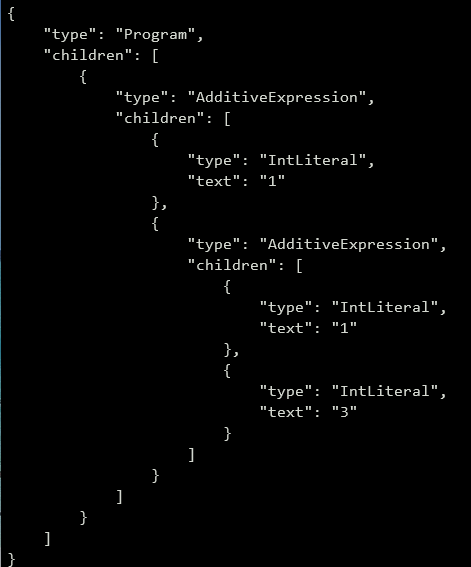
转迭代处理结合性问题
迭代中先处理左结合表达式
源码在 ast3 目录
/**
* 加法表达式处理
*
* @param {TokenReader} tokenReader
* @return {*}
* @memberof AST
*/
additive(tokenReader: TokenReader): any {
let left = this.primary(tokenReader);
let rootNode: ASTNode | null = left;
if (left) {
while (true) {
const peekToken = tokenReader.peek();
if (peekToken && peekToken.type === DfaState.Plus) {
const node = new ASTNode(ASTNodeType.AdditiveExpression);
tokenReader.read();
const right = this.primary(tokenReader);
if (right) {
node.addChild(left);
node.addChild(right);
// 处理完一个表达式存储为 根节点
rootNode = node;
// 保存当前节点为左节点,因为下一轮循环处理还有加法表达式的话
// 上一轮处理的根节点会变成这一轮节点的左节点
left = rootNode;
} else {
throw new Error('无法解析加法表达式!');
}
} else {
break;
}
}
}
return rootNode;
}输出示例:
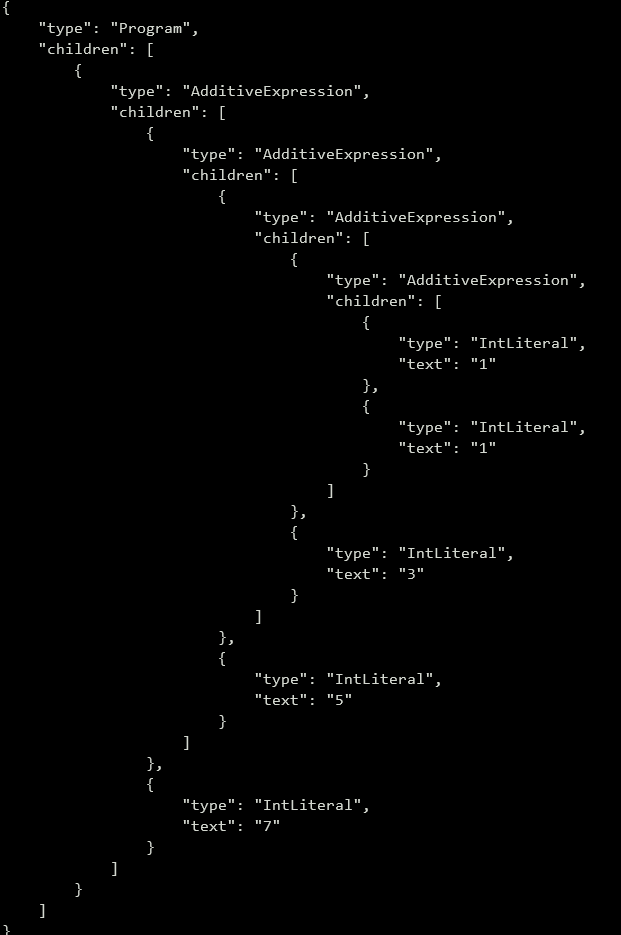
案例分析:乘法表达式
乘法表达式处理大体相似,不过它的优先级高于加法表达式
所以在处理加法表达式之前先去处理乘法表达式
1 + 3 \* 5 + 7;源码在 ast4 目录
/**
* 乘法表达式解析
*
* @param {*} tokenReader
* @return {*} {(ASTNode | null)}
* @memberof AST
*/
multiplicative(tokenReader: TokenReader): ASTNode | null {
let left = this.primary(tokenReader);
let root: ASTNode | null = left;
if (left) {
while (true) {
const peekToken = tokenReader.peek();
if (peekToken && peekToken.type === DfaState.Star) {
tokenReader.read();
const right = this.primary(tokenReader);
if (right) {
const node = new ASTNode(ASTNodeType.MultiplicativeExpression);
node.addChild(left);
node.addChild(right);
root = node;
left = root;
} else {
throw new Error('乘法表达式解析失败!');
}
} else {
break;
}
}
}
return root;
}
/**
* 加法表达式处理
*
* @param {TokenReader} tokenReader
* @return {*}
* @memberof AST
*/
additive(tokenReader: TokenReader): ASTNode | null {
let left = this.multiplicative(tokenReader);
let rootNode: ASTNode | null = left;
if (left) {
while (true) {
const peekToken = tokenReader.peek();
if (peekToken && peekToken.type === DfaState.Plus) {
const node = new ASTNode(ASTNodeType.AdditiveExpression);
tokenReader.read();
const right = this.multiplicative(tokenReader);
if (right) {
node.addChild(left);
node.addChild(right);
// 处理完一个表达式存储为 根节点
rootNode = node;
// 保存当前节点为左节点,因为下一轮循环处理还有加法表达式的话
// 上一轮处理的根节点会变成这一轮节点的左节点
left = rootNode;
} else {
throw new Error('无法解析加法表达式!');
}
} else {
break;
}
}
}
return rootNode;
}输出示例:

另外还有 减法、除法的,这里就不去一一实现了,我们简单实现了一下从 Token 构造 AST 语法树的思路
了解了递归下降分析算法,递归下降算法实现简单,容易理解跟调试,但是存在左递归、回溯问题
实际应用中使用的是一些优化算法例如: LL、LR、LALR、GLR 算法,不过这篇文章中不去展开学习这些算法
从分析中其实我们可以看到,表达式这种语法其实是有个固定结构的,我们可以用 一些公式描述
例如: exp + number、exp + exp、number + number
在实际应用中我们用上下文无关文法去描述语言语法
语法分析器
开源语法分析器
Bison:Bison是一个开源的LALR(1)语法分析器生成器,它可以根据文法来生成C、C++、Java等语言的语法分析器。它的语法类似于Yacc,可以使用BNF范式来定义语法规则
ANTLR:ANTLR是一个基于LL(*)算法的语法分析器生成器,可以生成Java、C#、Python、JavaScript等语言的语法分析器。它的语法类似于EBNF JavaCC:JavaCC是一个开源的Java语法分析器生成器,可以生成Java语言的语法分析器。它的语法类似于BNF PLY:PLY是一个用Python实现的语法分析器生成器,可以生成Python语言的语法分析器。它的语法类似于Yacc。 Yacc:Yacc是一个经典的语法分析器生成器,可以生成C、C++等语言的语法分析器。它的语法类似于BNF
我们这里使用 Bison 来做语法解析,资料比较多
Bison 在业界的一些应用:
mysql 的 sql 语法解析就用到了 Bison
在 mysql 源码中的 sql_yacc.yy 文件就是 Bison 规则文件
select_item_list 非终结符 是解析 select 参数列表

上下文无关文法
上下文无关文法(Context-Free Grammar,CFG)是一种用于描述形式语言结构的形式语法
为什么叫做上下文无关,一个CFG由四个部分组成:一个非终结符集合、一个终结符集合、一个起始符号和一组产生式规则
在CFG中,语法规则只涉及到单个非终结符的替换,而不考虑其所处的上下文环境,因此称为上下文无关文法
为什么?
CFG可以描述复杂的语言结构,包括嵌套结构、递归结构和条件分支等。
我们可以使用CFG来描述各种类型的编程语言、标记语言和数据格式等的语法规则,从而实现对这些语言的解析和处理
其次,CFG的计算效率比其他类型的文法更高
也就是说,大部分编译器的实现都是涉及 CFG 语法的,另外如果要自己实现 DSL 语言,需要先用 CFG 语法描述你的语言结构
BNF 文法
BNF 是 用来表示 CFG 的形式化语言
左边是非终结符,非终结符可以一直向下推导
右边包含的非终结符、终结符都可能有
中间是 文法写法 ::=
S ::= A + B
S ::= C + B
B ::= D文法类比
用我们使用的语言类比文法
<句子> ∷=<主语> <谓语> <宾语>
<主语> ∷=<名词>
<主语> ∷=<代词>
<谓语> ∷=<动词>
<宾语> ∷=<名词>
<宾语> ∷=<代词>
<代词> ∷= 我
<代词> ∷= 你
<动词> ∷= 吃
<动词> ∷= 做
<名词> ∷= 饭
<名词> ∷= 菜上述文法可以推导出
<句子> => <主语> <谓语> <宾语>
=> <代词> <谓语> <宾语>
=> 我 <谓语> <宾语>
=> 我<动词> <宾语>
=> 我吃<宾语>
=> 我吃<名词>
=> 我吃饭语法形式化的最终目的在于将语法分析的问题将装换成形式化的推导过程
Bison
bison 是一个词法分析器生成工具, 它将上下文无关文法转换为解析该语法的 C、C++代码
联合使用 flex 和 bison 可以实现一个编译器或解释器
案例分析:加法表达式
代码在 bison1 目录
示例
3 + 5 - 2;
3 + 5;
3;
3 - 2 + 5 - 1;文法
exp ::= INT
| exp Plus INT
| exp Minus INT词法分析
编写词法分析文件 calc.l
第一部分是头文件, 包的引入, 方法声明
第二部分%%包裹, 是 Token 正则匹配, 每个正则右边可以做一些逻辑处理, 比如值的存储
%option noyywrap
%{
#include <iostream>
#include "calc.tab.hpp" // 包含生成的 bison 头文件
#define YY_DECL int yylex()
%}
%%
[ \t] ; // ignore all whitespace
[0-9]+ {yylval.ival = atoi(yytext); return INT;}
\n {return NEWLINE;}
"+" {return PLUS;}
"-" {return MINUS;}
"exit" {return QUIT;}
%%语法分析
第一部分同样也是头文件区
第二部分:
token: 非终结符声明
type: 非终结符类型声明
left: 结合性规则, left 为左结合第三部分是文法, 由 %% 包裹
底部是一些模板代码, 也可以编写一些运行时代码
$$: 规则左侧的值
$n: 规则右侧第 n 个 token 的值
@$: 左侧位置信息
@n: 右侧第 n 个 token 的位置信息编写语法分析文件 calc.y
%{
#include <iostream>
#include <cstdlib>
using namespace std;
extern int yylex();
extern int yyparse();
void yyerror(const char* s);
%}
%union {
int ival;
}
%token<ival> INT
%token PLUS MINUS
%token NEWLINE QUIT
%left PLUS MINUS
%type<ival> expression
%start calculation
%%
calculation:
| calculation line
;
line: NEWLINE
| expression NEWLINE {
cout << "\tResult: " << $1 << endl;
}
| QUIT NEWLINE { cout << "bye!" << endl; exit(0); }
;
expression:
INT { $$ = $1; }
| expression PLUS INT { $$ = $1 + $3; }
| expression MINUS INT { $$ = $1 - $3; }
;
%%
int main() {
yyparse();
return 0;
}
void yyerror(const char* s) {
cout << "Parse error: " << s << endl;
exit(1);
}编译
Makefile 文件
all: calc
calc.tab.cpp calc.tab.h: calc.y
bison -d -o calc.tab.cpp calc.y
lex.yy.cpp: calc.l calc.tab.hpp
flex -o calc.lex.cpp calc.l
calc: lex.yy.cpp calc.tab.cpp calc.tab.hpp
g++ -std=c++11 -o calc calc.tab.cpp calc.lex.cpp
clean:
rm calc calc.tab.cpp calc.lex.cpp calc.tab.h calc.output编译并运行
# 编译
make
# 执行
./calc可以输入一些测试表达式,验证结果
// example1
1+2
// example2
1+2-3
// example3
1+9+2+4-5+2-9example3 执行结果

体验过文法生成编译器过程之后, 再来了解下不同的语法分析器所使用算法对我们文法的要求的区别
LL 算法
LL算法(Left-to-Right, Leftmost derivation)是一种自顶向下的语法分析算法,它使用预测分析法来进行语法分析。LL算法从起始符号开始,通过预测下一个产生式来构建语法分析树,直到达到输入串的结束
LL算法的优点是易于理解和实现,适用于一些具有相对简单结构的文法。
LL算法的局限性在于它对文法的要求较高,要求文法是LL文法,不能包含左递归,并且需要消除冲突和二义性
文法二义性
文法二义性指的是语法规则的定义中存在多个解析树的情况,导致解析结果不唯一
举个例子:
E -> E + E
E -> E \* E
E -> num解析方式一:
先乘后加
E
|
E + E
| |
E E * E
| |
num num解析方式二:
先加后乘
E
|
E * E
| |
E + E num
| |
num num
| |
2 4如何解决二义性的问题
- 在文法上消除二义性,调整产生式顺序、引入优先级和结合性规则等
- 引入括号或其他限定符明确表达式的结构,消除二义性
所以说 LL 算法实现的语法分析器对文法要求比较高
自顶向下-自底向上
自顶向下
先考虑总体,在考虑细节,将复杂问题分解为若干子问题逐步细化
在做递归分析的时候,我们是先识别整体,再逐步细化分析出当前整体的各个组成部分
自底向上
由简单到复杂,逐层向上构造,先从最基础的部分着手,一步步构造出整体
LR 算法
LR 算法是一种 "移进-规约" 的自底向上分析方法
核心思想是使用一个分析栈和一个输入缓冲区
移进(Shift): 从输入缓冲区读取一个终结符或非终结符,压入分析栈
规约(Reduce): 当分析栈顶部的符号与某个产生式的右部匹配时,执行规约操作
移进规约
举个例子:
用移进-规约方法分析 abbcde

移进-规约冲突
像前面的文法
E -> E + E
E -> E - E
E -> num在处理 1 + 2 - 3 时
处理 2 的过程可以选择规约
符合 E + E
也可以选择移进
符合 E - E
就会产生冲突
在 bison5 目录中编译会查看移进规约冲突错误信息
规约-规约冲突
对于下面的文法, X 可以规约为 U, 也可以规约为 V, 就会产生冲突
U -> X
V -> X
U -> XY
V -> Y案例分析:乘法表达式
代码在 bison2 目录
词法分析
补充 *、/ Token 的匹配
"*" {return MULTIPLY;}
"/" {return DIVIDE;}
"(" {return LPAREN;}
")" {return RPAREN;}文法
exp ::= term
| exp PLUS term
| exp MINUS term
term ::= factor
| term MULTIPLY factor
| term DIVIDE factor
factor: INT语法分析
新增 token 定义, 结合性约束
%token LPAREN RPAREN
%token PLUS MINUS MULTIPLY DIVIDE
%left PLUS MINUS MULTIPLY DIVIDE处理乘除法与加减法优先级,需要加入一层非终结符文法
exp:
term { $$ = $1; }
| exp PLUS term { $$ = $1 + $3; }
| exp MINUS term { $$ = $1 - $3; }
;
term: factor { $$ = $1; }
| term MULTIPLY factor { $$ = $1 * $3; }
| term DIVIDE factor { $$ = $1 / $3; }
;
factor: INT { $$ = $1; }
| LPAREN exp RPAREN { $$ = $2; }
;编译并运行
# 编译
make
# 执行
./calc输入一些测试表达式,验证结果
// example1
1+2*3/2
// example2
10-2*2-6/3
// example3
10-20*(3+2)+100/2example3 执行结果
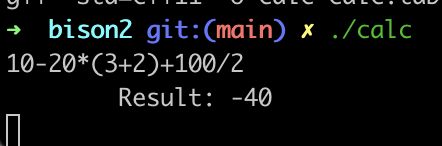
案例分析: SQL 解析
代码在 bison3 目录中
查询语句示例
select name from user;
select name,age from user;词法分析
代码在 bison3 目录中
关键字:select、from
变量识别:[a-zA-Z0-9_][a-zA-Z0-9]+
%%
select {return SELECT;}
from {return FROM;}
exit {return QUIT;}
[a-zA-Z0-9_][a-zA-Z0-9]+ {
yylval.strval = new string(yytext);
return ID;
}
, {return COMMA;}
\n {return NEWLINE;}
[ \t] ; // ignore all whitespace
%%文法
query ::= SELECT columns FROM table
columns ::= column
| columns ',' column
column ::= ID
table ::= ID语法分析
头文件:
引入了 string 包, vector 数组
#include <iostream>
#include <cstdlib>
#include <string>
#include <vector>
using namespace std;token 定义:
union 为 语法分析结果中的变量类型
%union {
std::string* strval;
std::vector<std::string>* strs;
int ival;
}
%token SELECT FROM ID COMMA
%token NEWLINE QUIT
%type <strval> table column ID
%type <strs> columns文法部分:
query: SELECT columns FROM table {
cout << "table:" << endl;
cout << "\t" << *$4 << endl;
cout << "columns:" << endl;
for(string col:*$2){
cout << "\t" << col << endl;
}
}
;
table: ID { $$ = $1; }
;
columns: column { $$ = new vector<string>(); $$->push_back(*$1); delete $1; }
| columns COMMA column { if($3!=nullptr){($1)->push_back(*$3);}; $$ = $1; delete $3;}
;
column: { $$ = nullptr; }
| ID { $$ = $1; }
;编译并运行
# 编译
make
# 执行
./calc测试验证:
# example1
select name,age from user
# example2
select account,pwd from user
# example3
select name,age,id, from userexample3 执行结果

案例分析:条件查询
代码在 bison4 目录中
示例
select id from user where name="xjq" and age="18"文法
conditions ::=
| WHERE condition_exp
condition_exp ::= condition
| condition_exp AND condition
condition ::= ID '=' factor
factor ::= STRING词法分析
条件查询相关 Token, 这里只支持 字符串查询
where {return WHERE;}
and {return AND;}
= {return ASSIGNMENT;}
\"[^\"\n]+\" {yylval.strval = new string(yytext);return STRING;}语法分析
类型定义: 结构体存储条件属性与值
struct Cond {
std::string attr;
std::string value;
};conds 数组存储多个条件
%union {
std::string *strval;
std::vector<std::string*>* strs;
std::vector<Cond*>* conds;
Cond* cond;
int ival;
}
%token SELECT FROM WHERE ID AND COMMA ASSIGNMENT
%token STRING
%token NEWLINE QUIT
%type <strval> query table column ID
%type <strval> factor STRING
%type <strs> columns
%type <conds> condition_expr conditions
%type <cond> condition文法:
query: SELECT columns FROM table conditions {
cout << "table:" << endl;
cout << "\t" << *$4 << endl;
cout << "columns:" << endl;
for(string *col:*$2){
cout << "\t" << *col << endl;
}
cout << "conditions:" << endl;
for(Cond *cond:*$5){
cout << "\tattr: " << (*cond).attr << endl;
cout << "\tvalue: " << (*cond).value << endl;
}
}
;
table: ID { $$ = $1; }
;
columns: column { $$ = new vector<string*>(); $$->push_back($1); }
| columns COMMA column { ($1)->push_back($3); $$ = $1; }
;
column: ID { $$ = $1; }
;
conditions: { $$ = nullptr; }
| WHERE condition_expr { $$ = $2; }
;
condition_expr: condition { $$ = new vector<Cond*>(); $$->push_back($1); }
| condition_expr AND condition { ($1)->push_back($3); }
;
condition: ID ASSIGNMENT factor {
Cond *cond = new Cond();
cond->attr = *$1;
cond->value = *$3;
$$ = cond;
delete $1;
delete $3;
}
;
factor: STRING { $$ = $1; }
;编译并运行
# 编译
make
# 执行
./calc测试验证:
# example1
select id from user where name="xjq"
# example2
select id from user where name="xjq" and age="18"
# example3
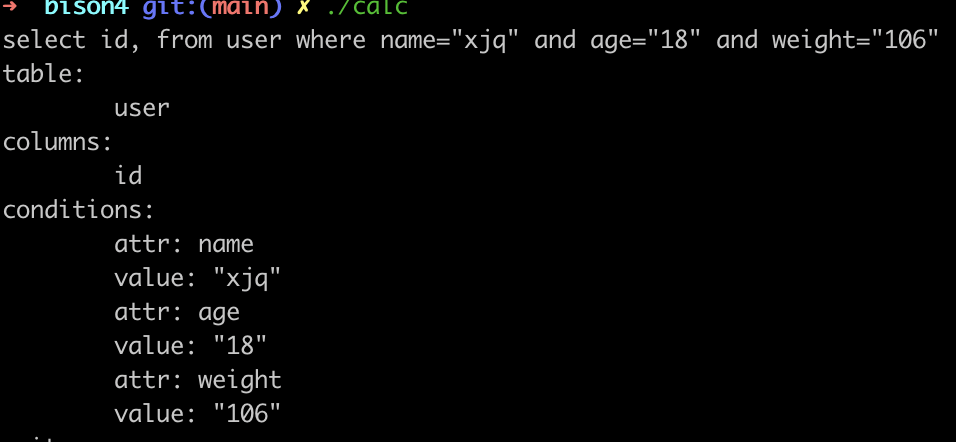
select id, from user where name="xjq" and age="18" and weight="106"example3 执行结果
扩展:正则的局限性
语法推导举个例子:一个表达式语法应该可能包含 +、-、*、/ 以及变量跟字面量等 Token,同时它们在语句中的位置也有一定规则,如何去描述这种规则是我们进行语法分析的第一步
比如这些事合法的表达式
a + 3 * 2这些就是非法的表达式,在语法分析阶段,需要给出错误,以及对应错误信息
3 ** 2 ++
3 / 2 +
* 3我们之前在词法分析中用正则表达式去描述 Token 很方便,但是在语法分析中会遇到一些问题
词法描述
// Token: Number
[0-9]+
// Token: Id
[a-zA-Z0-9_][a-zA-Z0-9_]*在语法分析里面,我们尝试去描述下面这些表达式
(109+2)
(1+(250+1))
(2+((20+5)-9))因为 状态机 只能维护有限数量的状态,所以这种多层括号嵌套的情况,正则已经没办法处理了
总结
作业
1. 词法分析
使用自己熟悉的语言实现一个词法分析器, 能够解析下面的表达式
1+2
1+2-3
1+2*3-1
1+2*(3+2)+10/22. 语法分析
使用自己熟悉的语言实现一个语法分析器, 能够解析加减乘除表达式, 得到 它们的 AST 结构
1+2
1+2-3
1+2*3-1
1+2*3+100/2